In the Dead of Night: The Quantum Hall Effect

Picture the High Magnetic Field Laboratory in Grenoble on the night of February 4 into February 5, 1980. The corridors are silent, save for the hum of a magnet pushing electrons into unfamiliar territory. German physicist Klaus von Klitzing ¹ leans over a silicon MOSFET (metal–oxide–semiconductor field-effect transistor), not expecting history to unfold in the dim hours before dawn. He has explained the course of detection and application in the Annual Review ².

At 2 a.m., Klitzing notices something extraordinary: the Hall resistance, which should trace a smooth linear slope, flattens into a plateau. Not a noisy plateau, not an approximate one—but exact, locked to a value of:

\[R_H = \frac{h}{e^2 \nu}\]

where $h$ is Planck’s constant, $e$ the electron charge, and $\nu$ an integer. Here, nature itself carved out precision: the resistance appeared quantized, stubbornly unaffected by impurities, temperature, or imperfections. By dawn, Klitzing realized he had uncovered a phenomenon of staggering exactness. In 1985, this discovery earned him the Nobel Prize in Physics.

---

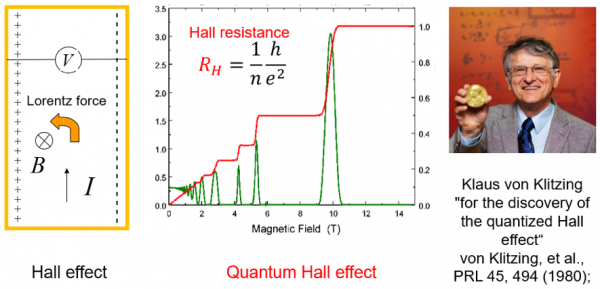
Figure 1: 2016 Nobel Prize in Physics-“topological phase transition and topological phases of matter.

---

The discovery wasn’t an accident—it was the marriage of three ingredients:

1. A two-dimensional electron gas (2DEG), engineered at semiconductor interfaces.
2. Strong magnetic fields, forcing electrons into cyclotron orbits.
3. Low temperatures, reducing thermal noise.

In these conditions, electrons don’t roam freely. Instead, their energy spectrum collapses into discrete rungs—Landau levels:

\[E_n = \hbar \omega_c \left(n + \tfrac{1}{2}\right), \quad n = 0, 1, 2, \dots\]

with cyclotron frequency $\omega_c = eB/m$. When the Fermi energy sits between Landau levels, the bulk is insulating, but the edges host conducting states. As the filling factor $\nu$ (the number of filled Landau levels) jumps discretely, the Hall conductance follows:

\[\sigma_{xy} = \nu \frac{e^2}{h}\]

—a relationship astonishing in its topological stability.

The integer quantum Hall effect (IQHE) redefined metrology. No longer would resistance be tied to fragile physical artefacts; instead, it became pinned to fundamental constants of nature. Today, $h/e^2$ (the von Klitzing constant) is a cornerstone of the International System of Units. But the impact went far deeper. Theoretical insights, especially Robert Laughlin’s argument in 1981, revealed that the quantization was not about material details but about topology—a robustness immune to small deformations. This was one of the first hints that condensed matter physics harbored topological phases of matter.

---

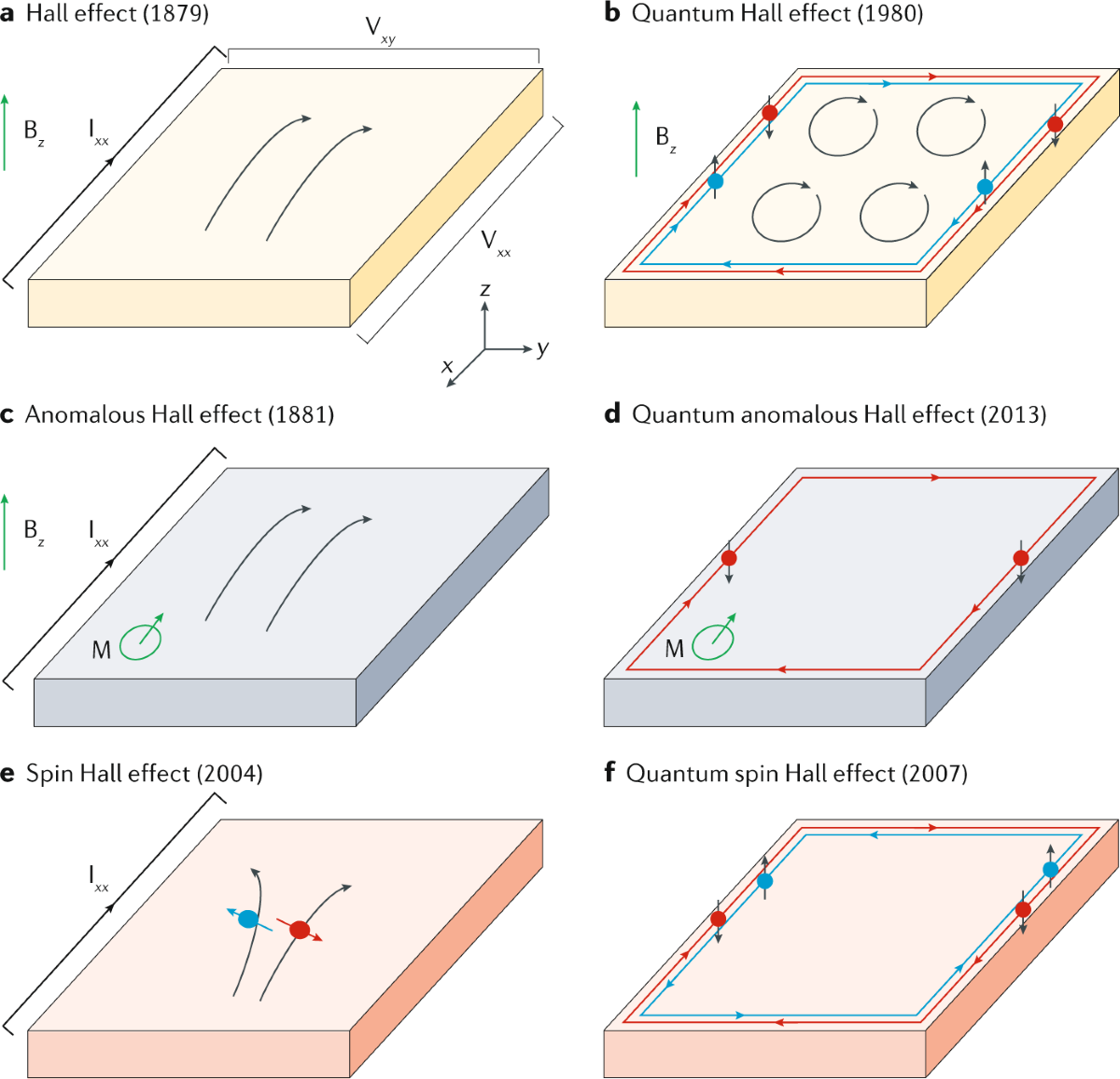
Figure 2: Landau levels and quantized Hall plateaus (Courtesy of Nature Reviews Physics).

---

Figure 3: Courtesy of Universe-Review.

---

In 1982, just two years later, Tsui, Stormer, and Gossard uncovered the fractional quantum Hall effect (FQHE). Here, strong electron–electron interactions gave rise to exotic quasiparticles carrying fractional charge and obeying statistics stranger than bosons or fermions: anyons. These discoveries shook the foundations of physics, opening doors to ideas that now underpin topological quantum computation. Robert Laughlin’s theoretical insight made clear that the quantization wasn’t about material specifics—it was about topology. Edge modes and bulk-boundary correspondence underscore how topology governs such “exact” effects. David Tong’s lecture notes walk through how Landau levels, Berry phases, and Chern–Simons theory weave together into this unified framework:

From Edwin Hall’s 1879 discovery of the classical Hall effect to Klitzing’s sleepless night in Grenoble, the story of the Hall effect is a tale of patience, precision, and serendipity. As physicist David Tong reflects in his lectures, the quantum Hall effect is “a gift from nature: an exact quantization accessible on a laboratory bench, a precision usually reserved for atomic physics.” It is a bridge between the tangible and the abstract, between experiment and topology. Physicist Steven Weinberg once remarked that “physics is the search for simplicity in the midst of complexity.” The quantum Hall effect epitomizes this: from the messy behavior of electrons emerges a law written in constants, exact and eternal.

The night of February 4th, 1980, reminds us that revolutions in science are not always loud. Sometimes, they appear in the quiet hum of a magnet, in the solitude of a lab at 2 a.m., when resistance itself decides to align with the fundamental symphony of nature.

---

---